Страница: 9/16
Рассчитываю средние значения по каждой группе:
=2769,56
=7120,57
=11308,17
17003,33
Таблица 4.3
Расчет коэффициентов вариации для групп,
полученных в результате простой группировки
|
№ группы |
Fj |
`x j |
å(xij -`xj )2 |
|`x j -`x | |
(`x j –`x)2 |
(`x j –`x)2Fj |
|
1 |
9 |
2769,56 |
5810420,00 |
4975,60 |
24756595,36 |
222809756,29 |
|
2 |
7 |
7120,57 |
15316291,71 |
624,59 |
390112,67 |
2730788,69 |
|
3 |
6 |
11308,17 |
8448304,83 |
3563,01 |
12695040,26 |
76170241,56 |
|
4 |
3 |
17003,33 |
1686962,67 |
9258,17 |
85713711,75 |
257141135,25 |
|
Итого: |
31261979,40 |
558851921,79 |
1) Групповая дисперсия (частная) – средний квадрат отклонений значения признака единицы совокупности в группе от их средней величины. Эта дисперсия характеризует вариацию признака в группе:
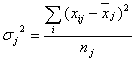, где
xij – значение признака i-й единицы i-й группы
`xj – частная средняя величина признака в i-й группе
nj - численность единиц i-й группы
2) Межгрупповая дисперсия – средний квадрат отклонений средних величин признака в каждой группе, называемых средней групповой, от средней общей для всей статистической совокупности в целом:
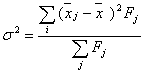, где
`xj – средняя i-й группы
xj – общая средняя
Fj – вес группы
J – количество групп
3) Внутригрупповая дисперсия – дисперсия, вычисляемая как средняя арифметическая средняя взвешенная из дисперсий, рассчитанных по каждой группе, на которые разбита статистическая совокупность:
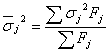, где
σj2 – групповая дисперсия j-й группы
5. Определение взаимосвязи между двумя показателями
(с использованием дисперсий).
Все явления общественной жизни взаимосвязаны и взаимообусловлены. Задача состоит в том, чтобы выявить и измерить связи и зависимости между изучаемыми явлениями.
Реферат опубликован: 31/10/2006