Страница: 4/7
Рис 4.
Итерация 3
Поиск направления. В точке х3= имеем Кроме того, множество активных ограничений в точке хз равно l = {2}, так что направление движения получается из решения следующей задачи:
Можно легко проверить по рис. 4. что действительно является решением этой задачи линейного программирования. Соответствующее значение целевой функции равно нулю, и процедура заканчивается. Более того, точка является точкой Куна—Таккера.
В этой конкретной задаче функция f выпукла, и по теореме 4.3.7 точка х является оптимальным решением.
Таблица 1
 |
Результаты вычислений по методу Зойтендейка для случая линейных ограничений
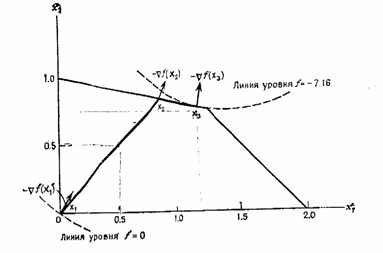 |
Рис. 5. Поиск решения методом Зойтендейка (случай линейных ограничений).
В табл. 1 приведены результаты вычислений для рассмотренной задачи. На рис. 10.5 изображен процесс поиска решения в соответствии с описанным алгоритмом.
Задачи с нелинейными ограничениями-неравенствами
Теперь рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств не обязательно линейных:
минимизировать f(х)
при условиях gi (х)£0, i=1, .,m.
В теореме формулируются достаточные условия, при которых вектор d является возможным направлением спуска.
 |
ТЕОРЕМА. Рассмотрим задачу минимизации f(х) при условиях gi (х)£0, i=1, .,m Пусть х—допустимая точка, а I—множество индексов активных в этой точке ограничений, т. е. . Предположим, кроме того, что функции f и gi для дифференцируемы в х, а функции gi для непрерывны в этой точке. Если при , то вектор d является возможным направлением спуска.
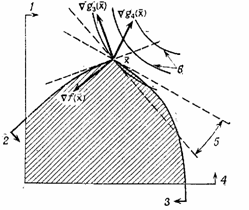
Рис. 6. Совокупность возможных направлений спуска в задаче с нелинейными ограничениями. 1— 1-е ограничение; 2—3-е ограничение; 3—4-е ограничение; 4— 2-е ограничение; 5— возможные направления спуска; 6— линии уровня целевой функции.
Доказательство. Пусть вектор и удовлетворяет неравенствам и при . Для выполняются неравенства , и так как gi непрерывны в точке х, то для достаточно малых . В силу дифференцируемости функций gi при имеем
где при . Так как , то при достаточно малых . Следовательно, при i = 1, . . .,m, т.е. точка допустимая для достаточно малых положительных значений . Аналогично из следует, что для достаточно малых > 0 имеем . Следовательно, вектор и является возможным направлением спуска.
На рис. 6 показана совокупность возможных направлений спуска в точке х. Вектор d, удовлетворяющий равенству , является касательным к множеству в точке х. Поскольку функции gi нелинейны, движение вдоль такого вектора d может привести в недопустимую точку, что вынуждает нас требовать выполнения строгого неравенства .
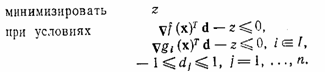 |
Чтобы найти вектор d, удовлетворяющий неравенствам для , естественно минимизировать максимум из и для . Обозначим этот максимум через z. Вводя нормирующие ограничения Для каждого j, получим следующую задачу для нахождения направления.
Реферат опубликован: 8/06/2009