Страница: 3/7
Основной этап. Шаг 1. Пусть задан хk. Предположим, что АT=(А1T, А2T), а bT=(b1T, b2T), так что . Взять в качестве dk оптимальное решение следующей задачи (заметим, что вместо этой задачи можно использовать Р2 или РЗ):
 |
Если , то остановиться; хk—точка Куна—Таккера, В противном случае перейти к шагу 2.
 |
Шаг 2. Положить равным оптимальному решению еле-., дующей задачи линейного поиска:
 |
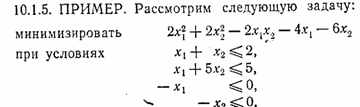где определяется в соответствии с (1). Положить , определить новое множество активных ограничений в и переопределить А1 и А2. Заменить k на k+1 и перейти к шагу 1.
Заметим, что . Решим задачу методом Зойтендейка, взяв в качестве начальной точки . Каждая итерация алгоритма содержит решение подзадачи, определенной в описании шага 1, для нахождения направления, а затем линейный поиск вдоль этого направления.
Итерация 1
 |
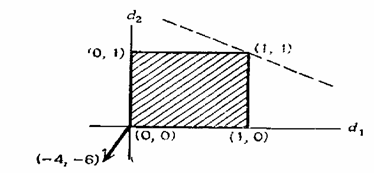Поиск направления. В точке имеем . Кроме того, в точке x1 активными являются только ограничения неотрицательности переменных, так что l = {3,4}. Задача для нахождения направления имеет вид
Рис. 2
Эту задачу можно решить симплекс методом для решения задач линейного программирования. На рисунке 2 показана допустимая область этой задачи.
Линейный поиск. Теперь, двигаясь из точки (0, 0) вдоль направления (1, 1), нужно найти точку, в которой значение целевой функции минимально. Любая точка может быть записана в виде , а целевая функция в этой точке принимает вид . Максимальное значение коэффициента l, для которого точка допустима, вычисляется по формулам и равно
Следовательно, если —новая точка, то значение получается из решения следующей задачи одномерной минимизации:
минимизировать —10+2
при условии 0£ £ .
Очевидно, что решением является , так что
Итерация 2
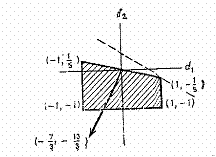Поиск, направления. В точке имеем .
Рис 3.
Кроме того, множество активных ограничений в точке х2 равно l={2}, так что направление движения получается из решения следующей задачи:
минимизировать
при условии
Читатель может проверить на рис. 3, что оптимальным решением этой задачи линейного программирования является точка , а соответствующее значение целевой функции равно .
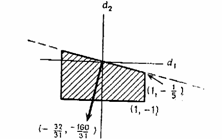
Линейный поиск. При начальной точке х2 любая точка в направлении d2 может быть представлена в виде Соответствующее ей значение целевой функции равно
Максимальное значение l для которого точка Х2+ld2 остается допустимой, определяется в соответствия с (1) следующим образом:
Таким образом, в качестве ^ берется оптимальное решение следующей задачи:
минимизировать
при условии
Оптимальным решением этой задачи является , так что
 |
Реферат опубликован: 8/06/2009