Страница: 6/14
и однородным граничным условием на свободной поверхности:
, (15)
где 
- вектор единичной нормали к поверхности.
Тогда для описания рассеяния волны на неоднородностях поверхности используется интегральное уравнение:
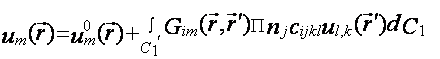, (16)
где точка 
находится внутри контура С, а точка 
лежит на С, 
- тензор Грина для смещений, П – скалярный дифференциальный оператор.
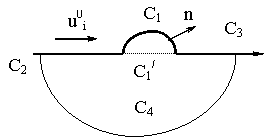
Физический смысл данного уравнения состоит в том, что оно описывает рассеянное поле, возникающее в результате действия на поверхность С2, С1/, С3 (рис.2) ненулевых напряжений, обусловленных наличием препятствий.
Ограничиваясь рассмотрением только изотропных твердых тел, для которых 
, перейдем к уравнению в потенциалах 
и 
.
Если рассматривать смещения только в плоскости xz, то векторный потенциал будет иметь лишь одну компоненту 
и соответствующее уравнение для вектора Ф
примет вид:
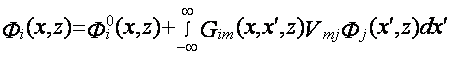, (17)
индекс m принимает значения x и z, 
- оператор возмущений.
Для малых препятствий наиболее простым методом решения данного уравнения является итерационный метод, в котором за нулевое приближение к решению 
выбирается поле падающей волны 
. Последующие приближения получаются подстановкой низших приближений в интеграл уравнения. В результате решение представляется в виде итерационного ряда (борновский ряд)
, (18)
Условие применимости борновского приближения накладывает ограничения на размеры и форму препятствий. В данном случае оно имеет вид:
<< 1, (19)
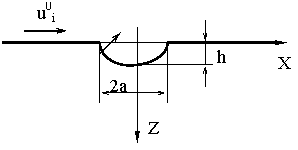
где 
функция описывающая дефект на плоской поверхности,
- максимальная глубина дефекта, 
- производная по 
функции описывающей профиль дефекта, 
, 
, 
- длина рэлеевской волны.
Можно произвести соответствующие оценки для фазового сдвига, связанного с увеличением пути, проходимого рэлеевской волной при огибании ею искривленной поверхности препятствия.
 | |||||||
 | |||||||
| |||||||
| |||||||
Реферат опубликован: 10/07/2008