On the problem of crystal metallic lattice in the densest packings

• Бесплатные рефераты
• Иностранные языки
• On the problem of crystal metallic lattice in the densest packings

Страница: 2/3

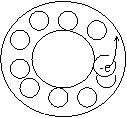
Roughly speaking, using the base cases of Born- Karman, let us consider a highly simplified case of one-dimensional conduction band. The first variant: a thin closed tube is completely filled with electrons but one. The diameter of the electron roughly equals the diameter of the tube. With such filling of the area at local movement of the electron an opposite movement of the ‘site’ of the electron, absent in the tube, is observed, i.e. movement of non-negative sighting. The second variant: there is one electron in the tube - movement of only one charge is possible - that of the electron with a negative charge. These two opposite variants show, that the sighting of carriers, determined according to the Hall coefficient, to some extent, must depend on the filling of the conduction band with electrons. Figure 1.

а) б)

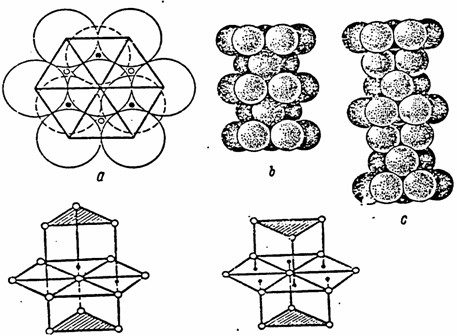
Figure 1. Schematic representation of the conduction band of two different metals. (scale is not observed).

a) - the first variant;

b) - the second variant.

The order of electron movement will also be affected by the structure of the conductivity zone, as well as by the temperature, admixtures and defects. Magnetic quasi-particles, magnons, will have an impact on magnetic materials.

Since our reasoning is rough, we will further take into account only filling with electrons of the conductivity zone. Let us fill the conductivity zone with electrons in such a way that the external electrons of the atomic kernel affect the formation of a crystal lattice. Let us assume that after filling the conductivity zone, the number of the external electrons on the last shell of the atomic kernel is equal to the number of the neighbouring atoms (the coordination number) (5).

The coordination number for the volume-centered and face-centered densest packings are 12 and 18, whereas those for the body-centered lattice are 8 and 14 (3).

The below table is filled in compliance with the above judgements.

Where Rh is the Hall’s constant (Hall’s coefficient)

Z is an assumed number of electrons released by one atom to the conductivity zone.

Z kernel is the number of external electrons of the atomic kernel on the last shell.

The lattice type is the type of the metal crystal structure at room temperature and, in some cases, at phase transition temperatures (1).

Conclusions

In spite of the rough reasoning the table shows that the greater number of electrons gives the atom of the element to the conductivity zone, the more positive is the Hall’s constant. On the contrary the Hall’s constant is negative for the elements which have released one or two electrons to the conductivity zone, which doesn’t contradict to the conclusions of Payerls. A relationship is also seen between the conductivity electrons (Z) and valency electrons (Z kernel) stipulating the crystal structure.

The phase transition of the element from one lattice to another can be explained by the transfer of one of the external electrons of the atomic kernel to the metal conductivity zone or its return from the conductivity zone to the external shell of the kernel under the influence of external factors (pressure, temperature).

We tried to unravel the puzzle, but instead we received a new puzzle which provides a good explanation for the physico-chemical properties of the elements. This is the “coordination number” 9 (nine) for the face-centered and volume-centered lattices.

This frequent occurrence of the number 9 in the table suggests that the densest packings have been studied insufficiently.

Using the method of inverse reading from experimental values for the uniform compression towards the theoretical calculations and the formulae of Arkshoft and Mermin (1) to determine the Z value, we can verify its good agreement with the data listed in Table 1.

The metallic bond seems to be due to both socialized electrons and “valency” ones – the electrons of the atomic kernel.

Literature:

Solid state physics. N.W. Ashcroft, N.D. Mermin. Cornell University, 1975

Characteristics of elements. G.V. Samsonov. Moscow, 1976

Grundzuge der Anorganischen Kristallchemie. Von. Dr. Heinz Krebs. Universitat Stuttgart, 1968

Physics of metals. Y.G. Dorfman, I.K. Kikoin. Leningrad, 1933

What affects crystals characteristics. G.G.Skidelsky. Engineer № 8, 1989

Appendix 1

Metallic Bond in Densest Packing (Volume-centered and face-centered)

It follows from the speculations on the number of direct bonds ( or pseudobonds, since there is a conductivity zone between the neighbouring metal atoms) being equal to nine according to the number of external electrons of the atomic kernel for densest packings that similar to body-centered lattice (eight neighbouring atoms in the first coordination sphere). Volume-centered and face-centered lattices in the first coordination sphere should have nine atoms whereas we actually have 12 ones. But the presence of nine neighbouring atoms, bound to any central atom has indirectly been confirmed by the experimental data of Hall and the uniform compression modulus (and from the experiments on the Gaase van Alfen effect the oscillation number is a multiple of nine.

Consequently, differences from other atoms in the coordination sphere should presumably be sought among three atoms out of 6 atoms located in the hexagon. Fig.1,1. d, e shows coordination spheres in the densest hexagonal and cubic packings.

Fig.1.1. Dense Packing.

It should be noted that in the hexagonal packing, the triangles of upper and lower bases are unindirectional, whereas in the hexagonal packing they are not unindirectional.

Literature:

Introduction into physical chemistry and chrystal chemistry of semi-conductors. B.F. Ormont. Moscow, 1968.

Appendix 2

Theoretical calculation of the uniform compression modulus (B).

B = (6,13/(rs|ao))5* 1010 dyne/cm2

Where B is the uniform compression modulus

аo is the Bohr radius

rs – the radius of the sphere with the volume being equal to the volume falling at one conductivity electron.

rs = (3/4 pn ) 1/3

Where n is the density of conductivity electrons.

Table 1. Calculation according to Ashcroft and Mermin

Table 2. Calculation according to the models considered in this paper

Of course, the pres

Реферат опубликован: 23/06/2009